は、一階の連立常微分方程式の例である。一般的な連立常微分方程式は、求積法で解くのは困難であるが、一般性を含む連立常微分方程式の例として、求積法で解ける連立常微分方程式が多少知られている 。 一例を挙げておく 。
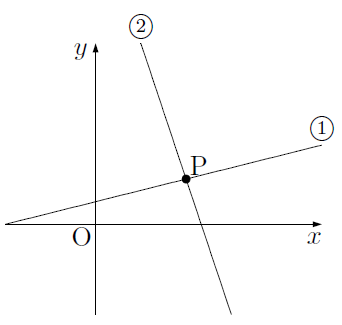
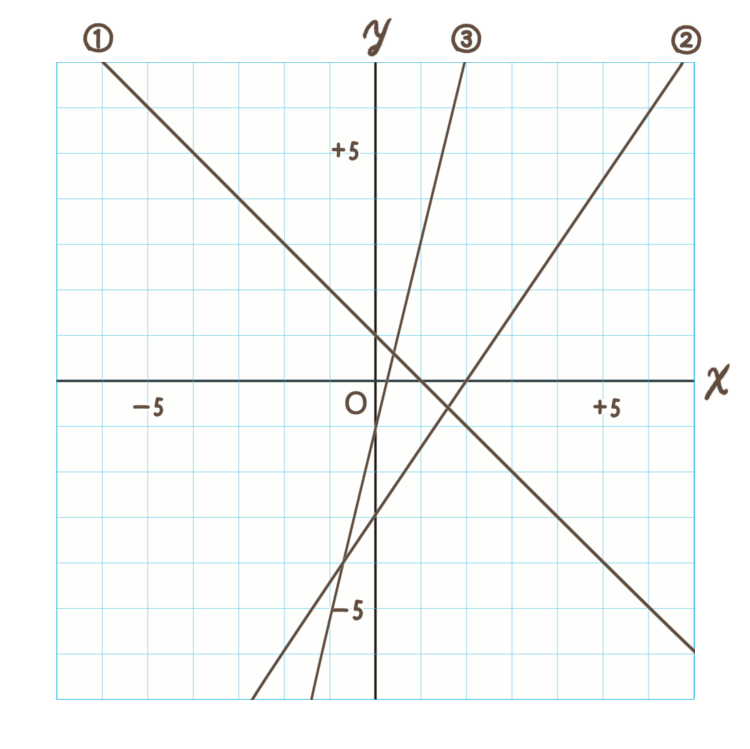
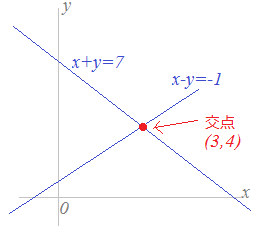
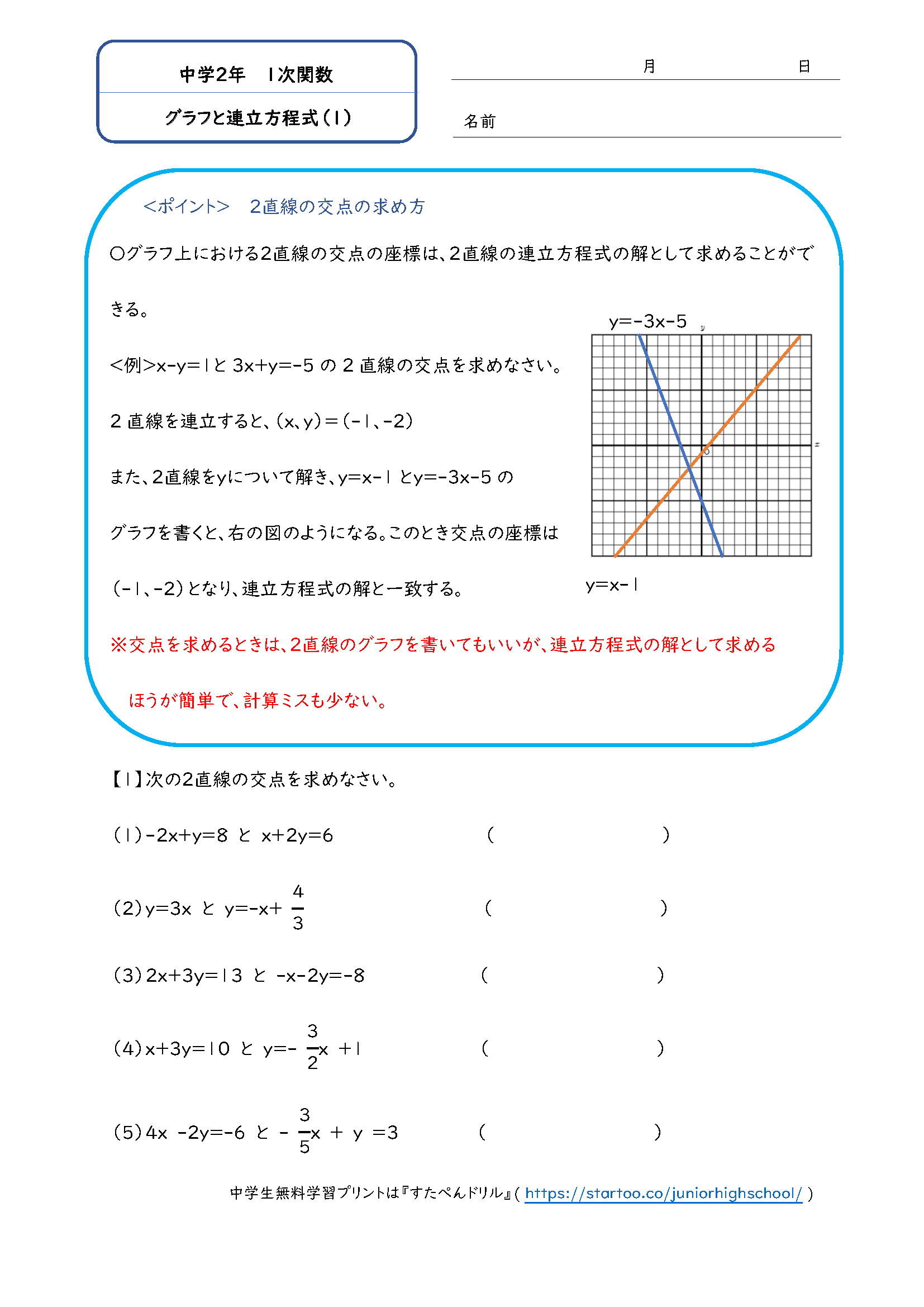
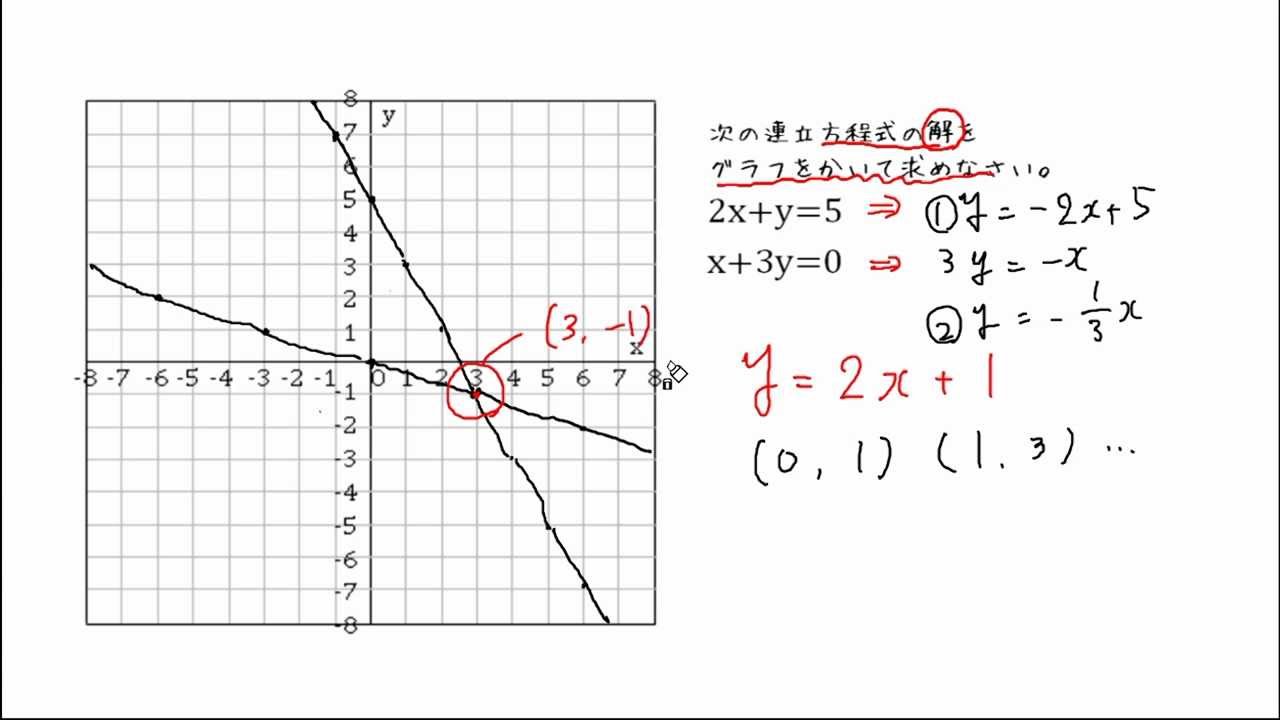
連立方程式 グラフ 解き方- 比熱が与えられているときは①を使う、熱容量を与えられているときは②を使います。 今回の問題では、金属球が熱を失うことになるのですが、その失った熱量は水・熱量計がもらうことになります。 なので金属球が失う熱量を直接求めることができない場合は、 水・熱量計が得た熱量か 連立一次方程式の係数を並べた行列を「係数行列 (coefficient matrix)」それに右辺の値を合体させた行列を「拡大係数行列 (augmented coefficient matrix)」といいます。 グラフ理論における有限グラフで,頂点間がつながっているかどうか,つながっているのであれ
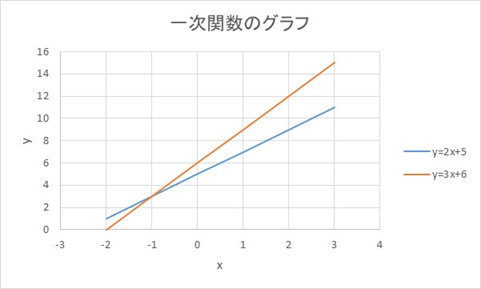
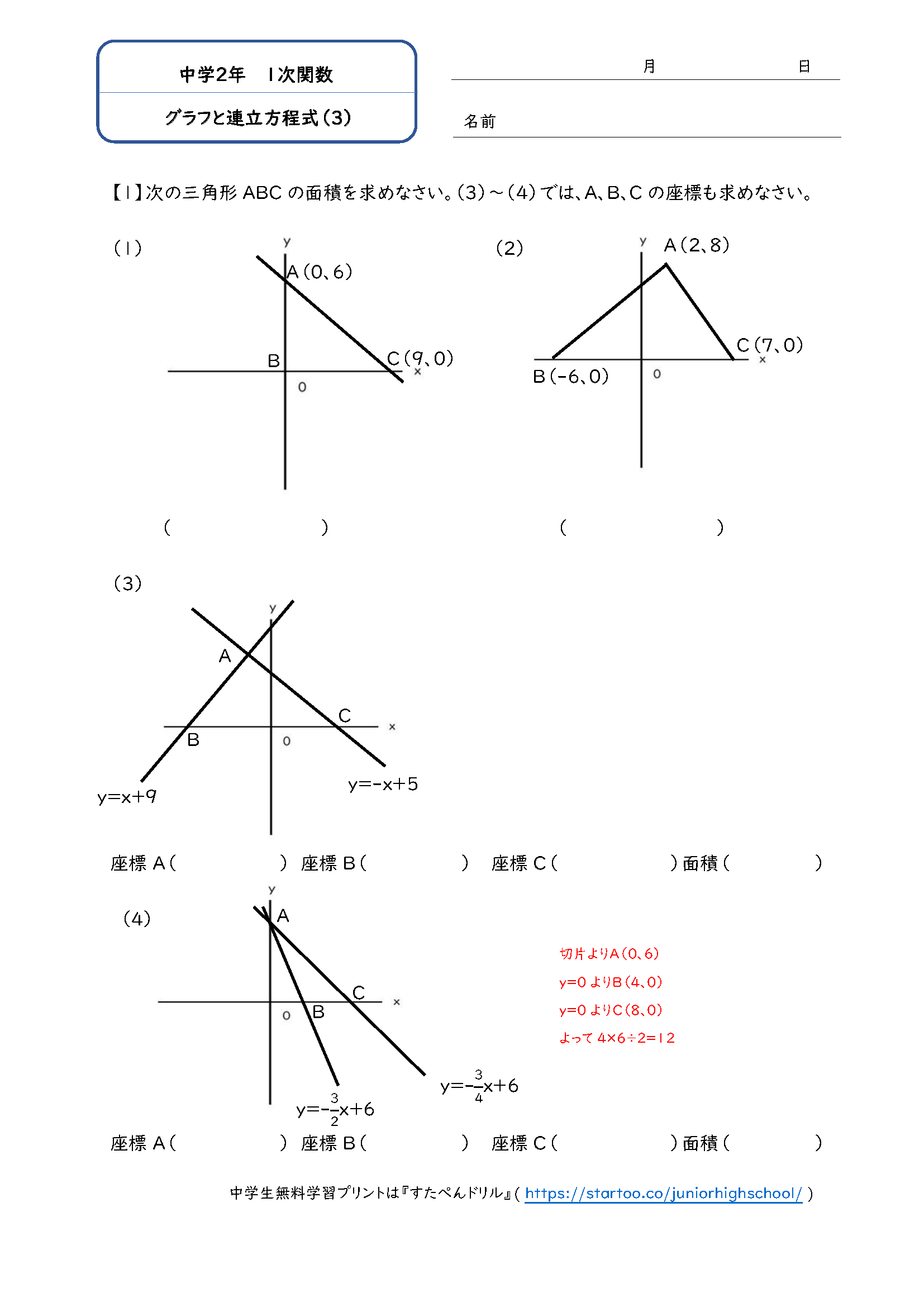
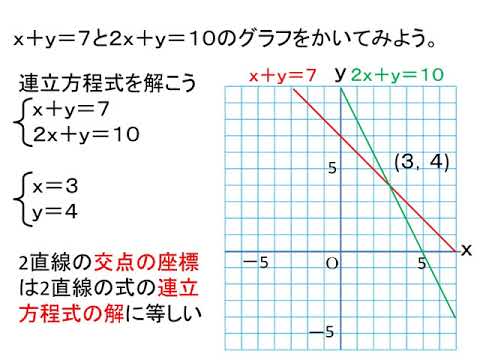
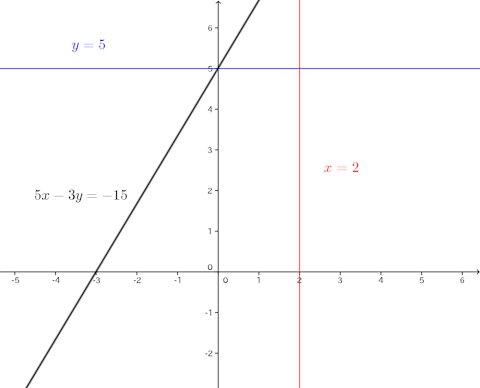
連立方程式 グラフ 解き方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  | |
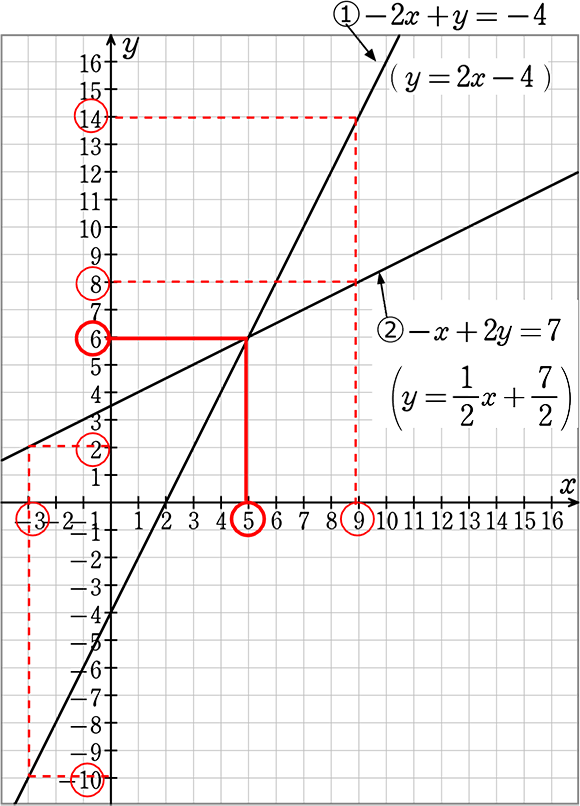
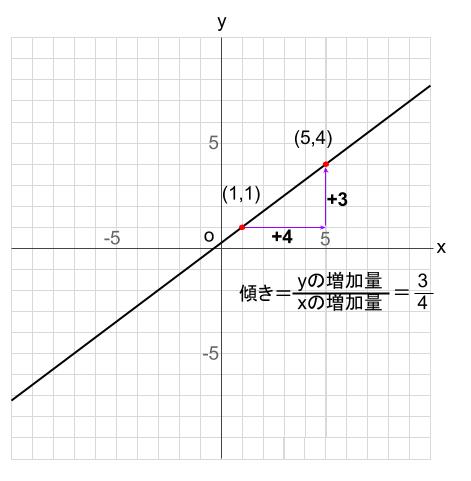
「連立方程式 グラフ 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
 | ||
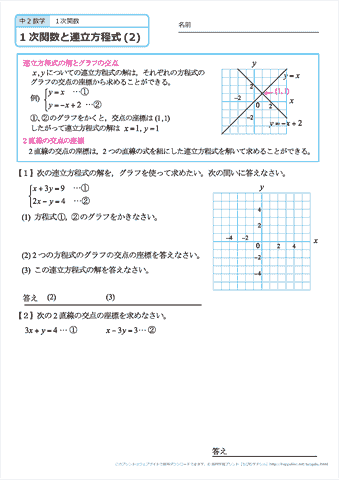
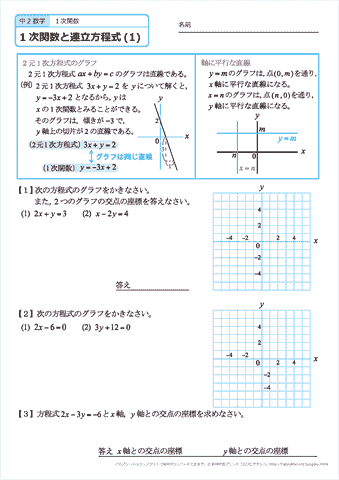
「連立方程式 グラフ 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  | |
「連立方程式 グラフ 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | ||
「連立方程式 グラフ 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | 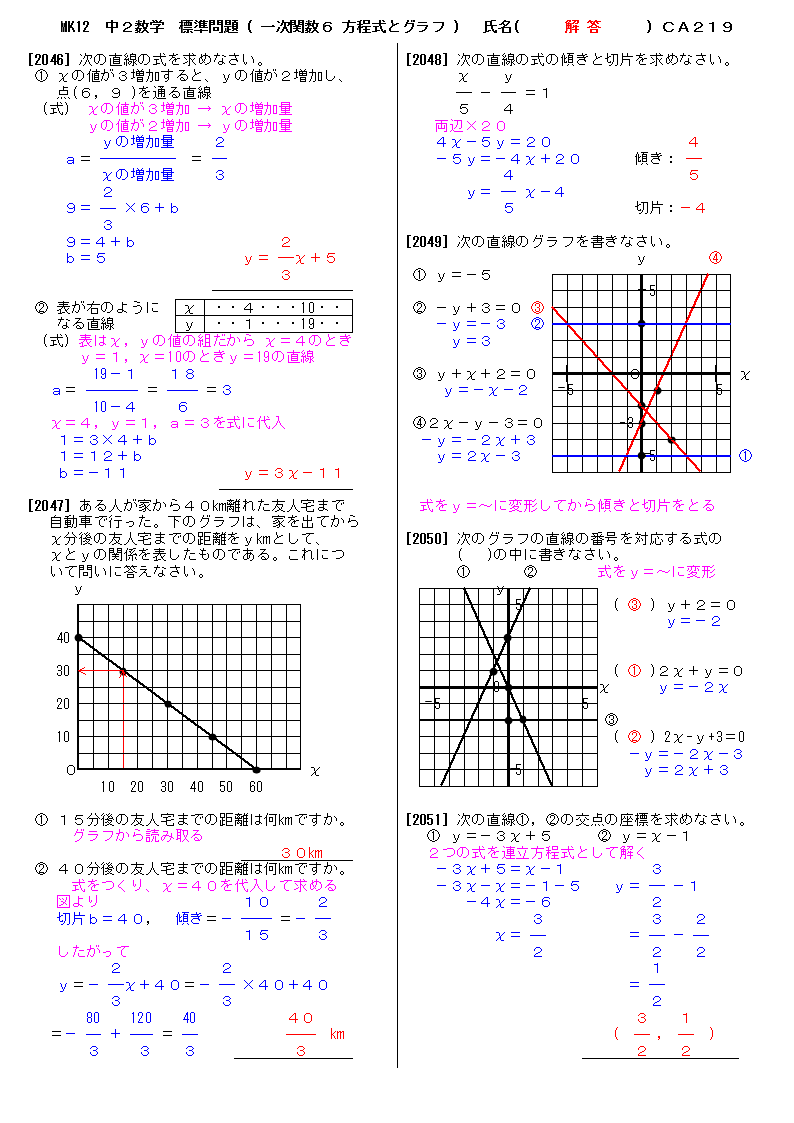 | |
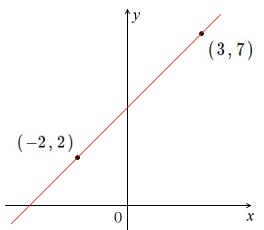 | 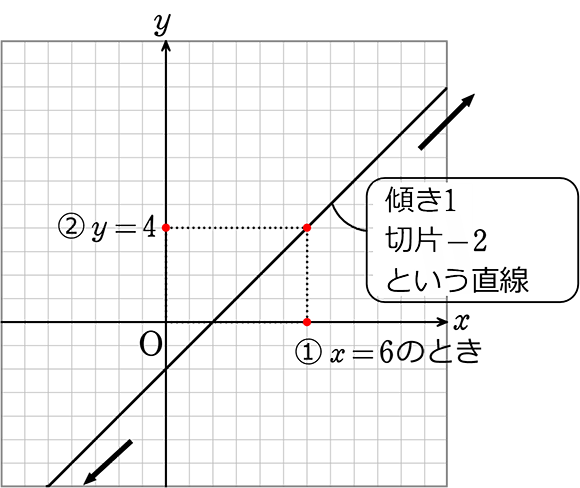 | |
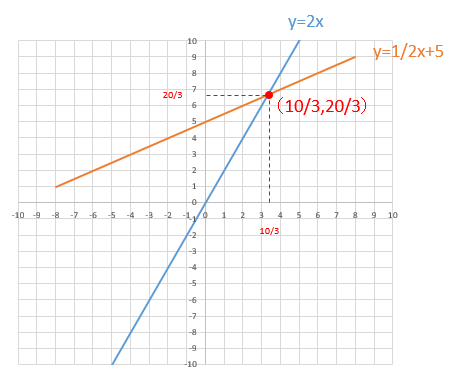
「連立方程式 グラフ 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「連立方程式 グラフ 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「連立方程式 グラフ 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
 |  | |
「連立方程式 グラフ 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |





0 件のコメント:
コメントを投稿