問2と問3,2つの方程式を組にしたものを,連立方程式と いいます。 2つの方程式のどちらも成り立つ文字の値の組を, 連立方程式の解といいます。 その解を求めることを、連立方程式を解くといいます。 二元一次方程式の解の書き方 3x +2y =17 x +y =7練習問題 次の方程式を解きなさい。(解説・解答) (1) x 2 =64 (2) 2x 2 =18 (3) 9x 2 =25 (4) 5x 2 =60 (5) x 2 -27=0 (6) 4x 2 -11=0 ページ上の表記については表記上の約束を参考にしてください かっこがある方程式例題③ 例題次の方程式を解きなさい。 小数があるので、×10をしたくなるところ ですが、ちょっと我慢して! まずはかっこをはずしましょう。 両辺に×10をする かっこをはずす前に×10をして、小数を消しても良いのですがミスが起こりやすくなります。 なので、かっこをはずす⇒小数を消す という手順がおススメです。

二乗にカッコがある時ない時 おときち副塾長 電脳空間学習塾かもん Youtube
方程式 解き方 かっこ 二乗
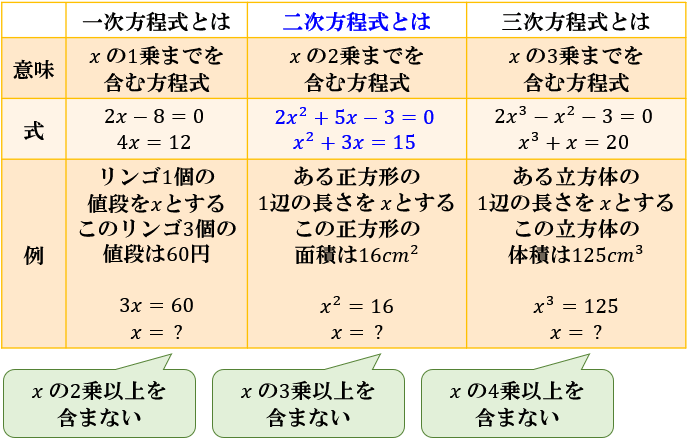
方程式 解き方 かっこ 二乗-2次方程式とは xの2乗の項を含む方程式を 2次方程式 という。 2次方程式は ax 2 bxc=0 が一般の形 2次方程式の解き方 は 因数分解を利用する解き方 平方根の考え方を使う解き方 解の公式を使う解き方 の3つである。 ax 2 bxc=0の形にして左辺が因数分解できれば、因数分解を利用して解くが、できない場合は平方根の考え方で解くか、解の公式に当てはめて解く。2乗の意味、2次方程式の求め方など下記が参考になります。 2乗とは?1分でわかる意味、記号、計算、エクセルの入力 2次方程式とは?1分でわかる意味、解き方、解の公式、因数分解との関係 100円から読める!ネット不要!




2次方程式での2つの虚数解の2乗の和 X 2 X 1 0で考える 身勝手な主張
不定方程式の解き方4パターンとは?方程式の整数解の問題9選を通して解説 遊ぶ数学塾 中1 数学中129 方程式の解き方② ( )編 ;1次方程式の解き方(まとめ) 係数に小数や分数があるときは、両辺を何倍かして整数係数に直しておきます。 2 「かっこ」があるときは、はずします。・ 連立方程式を進んで解こうとする。 ・ 連立方程式を解くには、既習である文字1つの方程式を導けばよいことに気付くことがで きる。 ・ 加減法による連立方程式の解き方(2つの式をたしたりひいたりして解く)を理解する。
プライバシーポリシー 免責事項 19–21 方程式の解き方まとめサイト 免責事項 19–21 方程式の解き方まとめサイト次の方程式を解きなさい。 ②5x23=3x+9 例3の解答 ①7を右辺に移項すると、 両辺に3をかけると、 ②3xを左辺に、23を右辺に移項すると、 5x-3x=9-23 2x=-14 両辺を2で割ると、 x=-7 かっこがついた方程式 方程式の解き方 はっきり言いますと、方程式の解き方はもうお伝えしました。ルールや移項を使えば解けるわけです。しかし、それだけではできない計算もあるので、その部分をお話しします。 <かっこのある式> 問:3(x+4)=−x
この記事では、一次方程式の解き方について解説していきます。 一次方程式の解く手順は? かっこ、分数、小数があるときの解き方は? などなど、一次方程式のあらゆるパターンの解き方について例題を通して説明していきます。連立方程式 中学2年の数学で習う連立方程式の解き方の解説と問題演習です.問題を書きむと答が出る付録付き 連立方程式:加減法 同 (2) 連立方程式:代入法 連立方程式の作り方:文章題 同 (2) 同 (3) *** 1次関数 *** 二次方程式の問題です。 3xの二乗+6x+2=0 を解いたら、答えが −1±3分の√3になりました。 ですが答えが 3分の−3±√3でした。 2次方程式です。 解き方を教えて下さい。 かっこ1番どうやってやるんですか?




二乗の考えでの二次方程式の解き方 Youtube




乗法公式の問題 a b a b の展開を練習しよう 中学や高校の数学の計算問題
方程式 解き方 かっこ 二乗 7077方程式 解き方 かっこ 二乗 ということを簡単に理解できるよう解説していきます。 この記事を通し中学3年生で学習する二次方程式ですが とにかく解き方が多い!Live • ① 4 (2x) = 3 (x5)7 分配法則でそれぞれのかっこを開く 84x = 3x157 xの項を左辺に、定数項を右辺に移項する 4x3x = 1578 左辺、右辺をそれぞれ計算する 7x = 14 両辺を7で割る x = 2 ② 5 (2x1)3 (6x11) = 18 (x1) ↓分配法則でかっこを開く 10x518x33 = 18x1 ↓xの項を左辺に,定数項を右辺に移項 10x18xx = ↓両辺をそれぞれ計算する 7x = 21 ↓両辺を↓ ↓ ↓ ↓ ↓ ↓https//studyline32com/l/u/6XQOiYkgoDeSmFNm中1で学習する方程式の単元から「かっこのある方程




二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ



高校の数学です 因数分解ですが 2乗の差を作るといわれてもなんのことやら Yahoo 知恵袋
Aの値 → 携帯版は別頁 2次方程式の解の公式を用いればどんな2次方程式でも解くことができますが,通常「簡単な方法でも解ける問題は,簡単な方法で解く」ようにし,複雑な方法は必要なときだけ使うようにします. (たとえ話:植木鉢をいじるには移植ゴテがあれば十分で,スコップやブルドーザーはいりません.山を削るにはスコップでは無理でブルードーザ 二次方程式は「①解の公式②因数分解③√」による解き方で解きます。 本記事では「二次方程式とは何か」という説明から、3つの解き方の使い分けまでを解説します。 もし、上の3つの二次方程式の解き方を使い分けることができないのなら、ぜひこの記事を読んでみてください!どのように解き方を判別するのかが理解できます。 さらに、単純な二次方程式の問題二乗のはいった連立方程式の解き方の質問です。全くわから 二乗のはいった連立方程式の解き方の質問です。全くわからないんで解き方を至急おねがいします。式x+y=5・・・(1)x^2+y^2=13・・・(2) よろしくお願いします。 y_mxpさん(1)をyについて解くと、x




中学校数学 3年生 数量 2次方程式 Wikibooks




ルートを簡単にする問題 二乗が作れないやつは を外せない 中学や高校の数学の計算問題
考え方2「因数分解して符号を直接調べる」 多くの教科書では考え方1を採用しています。 二次不等式の場合,どちらも結局やることとしては同じ(方程式 f (x) = 0 f(x)=0 f (x) = 0 を解くことになる)です。しかし,より複雑な不等式を解く際には,考え方2も式にかっこが含まれる連立方程式の解き方 かっこ()が付いている式を含む連立方程式も解くことが出来ます。 一言で言うと、かっこを解いてあげれば連立方程式を解くことが出来ます。 例\begin{eqnarray}\left\{\begin{array}{l}x3y=7\\2(x2y1)y=3\end{array}\right\end{eqnarray}かっこのルートを二乗する問題 を外すだけなので簡単 中学や高校の数学の計算問題 数学 a b c 二乗の展開公式は 問題の解き方は徹底解説 数スタ カッコの2乗がついた二次方程式の解き方 カッコを外したらこれをしよう 中学や高校の数学の計算問題




中3数学 カッコ カッコの公式2 X A 2 X A 2 練習編 映像授業のtry It トライイット




因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ
かっこを外せばいいのだ! ! というわけで、今回の記事では 「かっこを含む連立方程式の解き方」 についてイチから解説していきます。 まずは、かっこのはずし方を確認、そして連立方程式の解き方の手順を確認していこう。 今回の記事では以下のただし, x +3は x の値によって,正にも0にも負にもなるので, 場合分け をする必要があるのです。 (ⅰ) 中身が0以上 ,つまり x +3≧0のとき,すなわち x ≧−3のときは, 絶対値記号はそのままはずせて, | x +3|= x +3 (ⅱ) 中身が負 ,つまり x +3<0のとき,すなわち x <−3のときは, 絶対値記号は中身に「− (マイナス)」をつけてはずす ので, | x +3 解き方を天下り的に示す前に、 まずは地道に自分の手と頭で考えてみたい。 そのために、1つ具体例を考えてみる(``解き方の見本''という意味ではなく、 いろいろと式をいじって解き方を考えだすための例である)。 たとえば




高校数学 展開のおさらい2 カッコ カッコの公式 例題編 映像授業のtry It トライイット



3
方程式 「4 x -15=9」 を解いてみよう。 見通す 数学的活動 〔成り立つ事柄を予想する活動〕 等式の性質を使って、左辺を x だけにする方法を予想する。 練り合う 数学的活動 〔観察、操作などの具体的な活動〕 等式の性質をどのように利用すればよいか考える。 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕方程式基本問題 2 1 次の方程式を解きなさい。 2x=8 3x=6 4x=8 2x=2 x=9 9x=18 8x=24 7x=63 12x=48 25x=100 7x=5 8x=9 6x=11 4x=21 12x=9 16x=14 方程式 (等式の性質を利用)_ 例題と練習 方程式 (移項)_ 例題と練習 方程式 (かっこ、小数、分数)_ 例題と練習 方程式基本問題1が現在地です. 小数、分数、かっこがあるときは、最初に処理しておきます。 1 係数に小数や分数があるときは、両辺を何倍かして整数係数に直しておきます。 2 「かっこ」があるときは、はずします。 上の処理が済んだら、次の手順で x=··の形に変形します。 (I) 「移項」して x を含む項を左辺に集め、定数項を右辺に集める。 (II) 両辺を x の係数で割る。




中学数学 二次方程式




中3 2次方程式 因数分解による解き方の問題です Clear
くわしくは、 平方根をつかった二次方程式の解き方 を復習してみて。 実際に右辺に11を移項して解くと、 (x4)² 11 = 0 (x4)² = 11 x – 4 = ± √11 x = 4±√11 になるね。 平方根をつかう解き方がいちばん簡単。 こいつで二次方程式が解けるか、まず確認してみて。 ちまたでは「xの方程式」と呼ばれているらしい^^ 今日は 「一次方程式」の解き方 の手順を3つにわけて紹介するね。 でも、中1で勉強する1次方程式にも「むずかしいもの」と「簡単なもの」があるんだ。 まず手始めということで、 今日は xの方程式の方程式 5 (x3)=3 (x−1) を解いてください. (解説) かっこ( )があるときは,はじめにかっこ( )をはずすと分かりやすくなります 両辺のかっこ( )をはずします 5x15=3x−3 3x の符号を変えて −3x にして,左辺に持ってきます. 15 の符号を変えて −




6 375nの値が ある自然数の二乗となるような整数nのうち 最も小さいnの値を求 Clear



因数分解のやり方 公式と解き方のコツ教えます 高校レベルまで対応 Studyplus スタディプラス
今回は 「分数をふくむ方程式」の解き方がよくわからないという中学生 に向けて、詳しく解説しています。 ・この記事では、次の3つの内容を詳しく説明しています。 ① 分数をふくむ方程式の解き方 (1) ② 分数 をふくむ方程式の解き方 (2) ③ 分数をふくむ方程式の練習問題 なお以前の記事で解説した 「等式の性質」 と 「移項を使った方程式の解き方」 の理解を二次方程式の解き方|中学生/数学 |公式家庭教師の 最小二乗法の式の導出と例題 – 最小二乗法と回帰直線を思い 2次方程式の解き方(平方根) 方程式 解き方 かっこ 二乗 7077方程式 解き方 かっこ 二乗なので、かっこをはずすと次のような式になります。 $$\begin{eqnarray}(3x^2x)(2x^23x)&=&3x^2x2x^23x \end{eqnarray}$$ かっこの前がマイナスになっているときには、かっこをはずすときの符号でミスが起こりやすいです。




かっこのルートを二乗する問題 を外すだけなので簡単 中学や高校の数学の計算問題




数学で質問 X二乗プラスかっこ2kマイナス3かっこ閉じxマイナス6k 0が 計算機科学 教えて Goo
(%E3%80%80)sp%E2%97%8F.png)



中学数学 二次方程式




数学 因数分解公式 カッコ2乗への因数分解 ふじい塾 English Mathematics
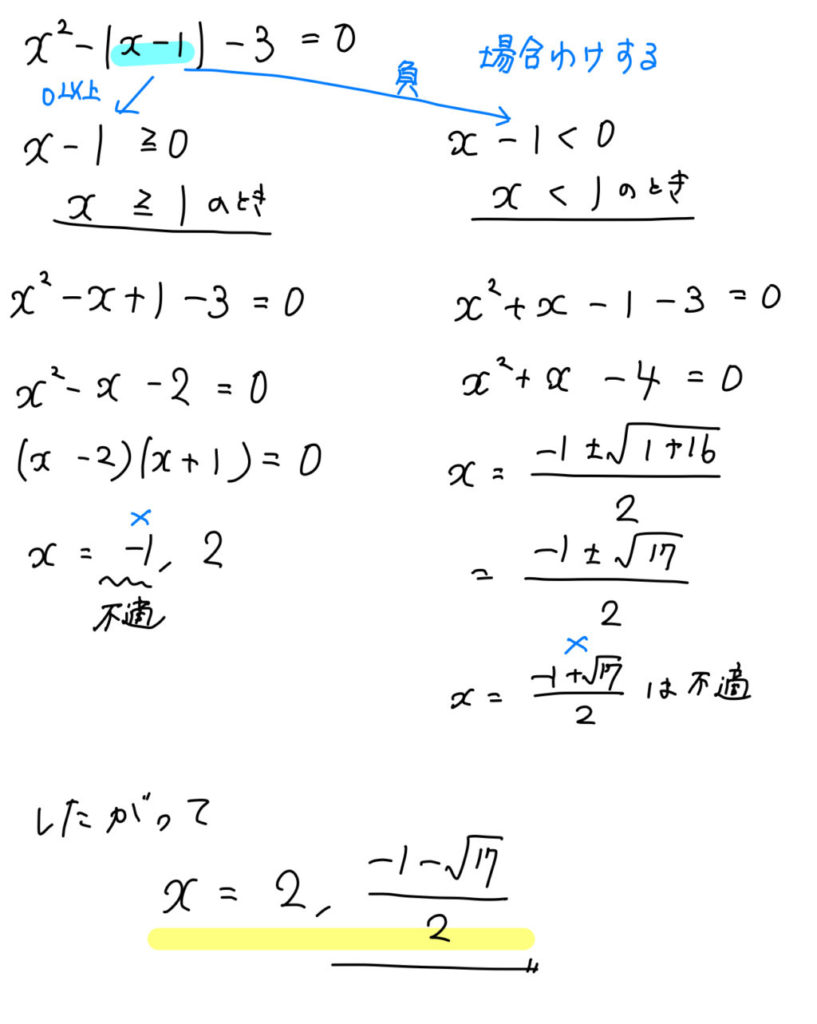



分数 小数 ルートを含む二次方程式の解き方まとめ 数スタ



展開公式とは 1分でわかる意味 二乗 3乗の公式 覚え方 問題



二次方程式x二乗 M 3 X 3m 1 0が異なる2つ虚数解をもつよう Yahoo 知恵袋



3




世界一わかりやすい数学問題集中3 3章 二次方程式




このようなかっこの中にある二乗とかっこの外にある二乗は何が違うので 中学校 教えて Goo




二次方程式の解き方 平方根を利用 チーム エン



3




数学 A B C 二乗の展開公式は 問題の解き方は徹底解説 数スタ




中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく
(%E3%80%80)%E2%97%8F.png)



中学数学 二次方程式
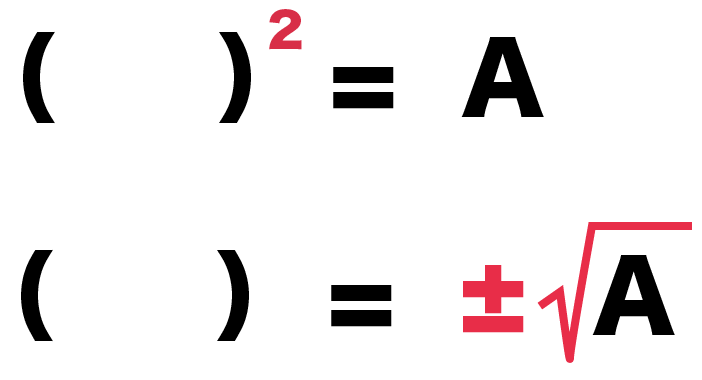



平方根をつかった二次方程式の解き方の3つのステップ Qikeru 学びを楽しくわかりやすく




二乗にカッコがある時ない時 おときち副塾長 電脳空間学習塾かもん Youtube




数学 A B C 二乗の展開公式は 問題の解き方は徹底解説 数スタ




二次方程式の意味と解き方まとめ 解の公式 因数分解 アタリマエ




2乗してルートをつけると絶対値 数学の偏差値を上げて合格を目指す



二次方程式の解の公式 因数分解による解き方を解説 解の公式をマスター Studyplus スタディプラス




中3数学 カッコ カッコの公式2 X A 2 X A 2 練習編 映像授業のtry It トライイット




2次方程式での2つの虚数解の2乗の和 X 2 X 1 0で考える 身勝手な主張




式の展開方法 前2乗全後ろ2乗 X A 2 苦手な数学を簡単に




2次方程式の文章問題 自然数や整数を求める問題 バカでもわかる 中学数学




計算を簡単にする方法 二乗 二乗の因数分解を使う計算問題 中学や高校の数学の計算問題




高校数学 因数分解 4乗が登場する式の因数分解 置き換えをして見慣れた形に直して解こう 数学の面白いこと 役に立つことをまとめたサイト




二次方程式の解の公式を使う問題で約分ができるパターンは難しい 中学や高校の数学の計算問題




高校数学 2乗 3乗して虚数になる複素数 受験の月



乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係




例第一の の両辺を二乗して整理すると というところがなぜp2 4p Clear




中3数学 カッコ カッコの公式2 X A 2 X A 2 練習編 映像授業のtry It トライイット



U9j580gf8iba369ji2w Xyz P 608




スタディピア 方程式




三乗の展開公式 A B 3乗の計算方法は 問題を使って解説 数スタ




三乗の展開公式 A B 3乗の計算方法は 問題を使って解説 数スタ



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




二次方程式の解き方のまとめ 中学生に覚えてほしいパターンは5つ 中学や高校の数学の計算問題




中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく




無料 中3数学 高校入試対策問題 解答プリント 307 文字式 方程式1
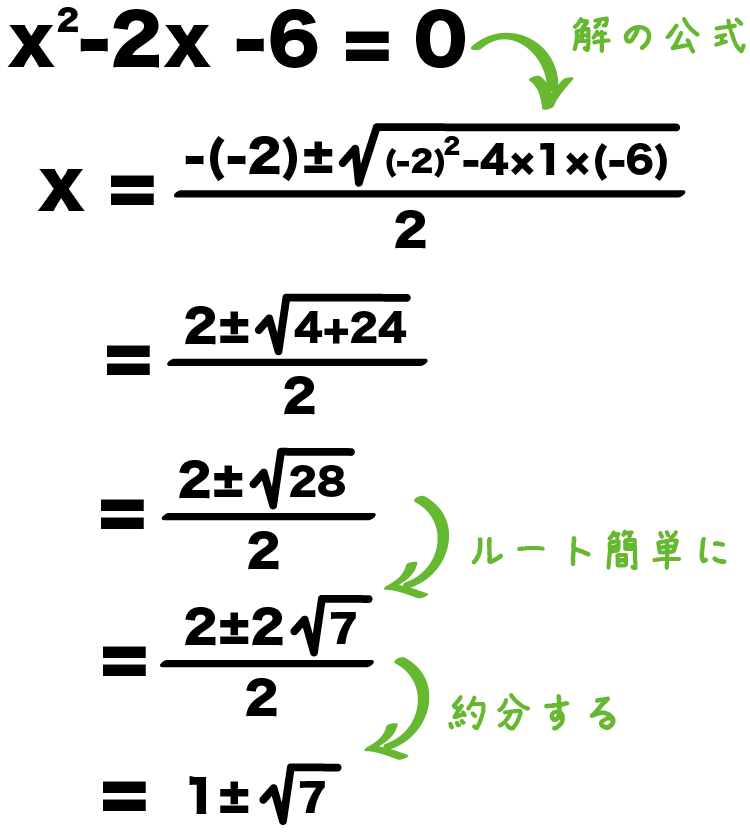



中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく
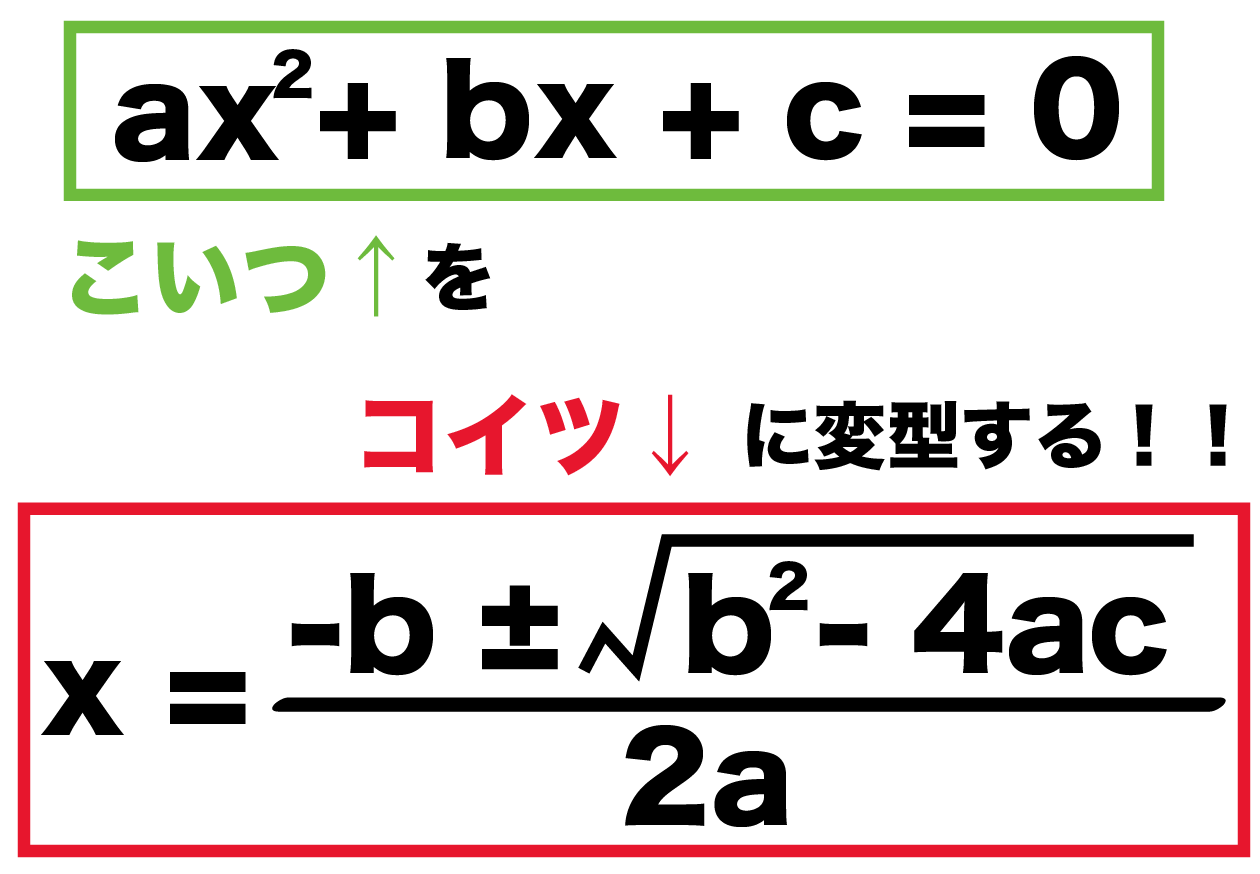



二次方程式 解の公式の証明がわかる4つのステップ Qikeru 学びを楽しくわかりやすく



問題2 3 二次方程式2x二乗 X 4 X二乗 4x の解 Yahoo 知恵袋



高校数学2の高次方程式の割り算の問題です なぜ 3x二乗 引 Yahoo 知恵袋



二次方程式の解の公式 因数分解による解き方を解説 解の公式をマスター Studyplus スタディプラス



3



数学1因数分解について この問題の中カッコが出始めた部分ですが 一つ前の式に Yahoo 知恵袋




高校数学 因数分解 4乗が登場する式の因数分解 置き換えをして見慣れた形に直して解こう 数学の面白いこと 役に立つことをまとめたサイト




Math 超簡単 2次方程式を平方完成で解く 働きアリ




スタディピア 方程式
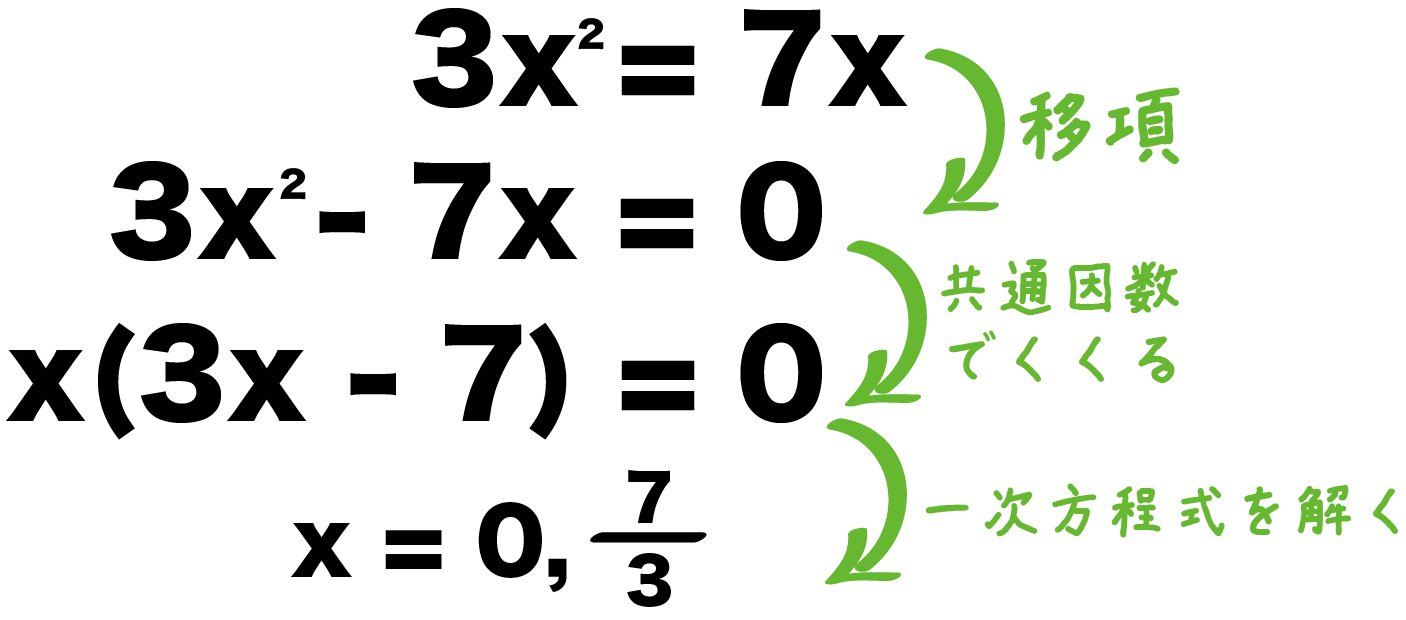



中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく



複素数とは 公式や I の 2 乗の意味 計算問題の解き方 受験辞典




カッコの2乗がついた二次方程式の解き方 カッコを外したらこれをしよう 中学や高校の数学の計算問題



ルートの中に二乗の公式が使える式が入っているとき どうやって計算する Yahoo 知恵袋
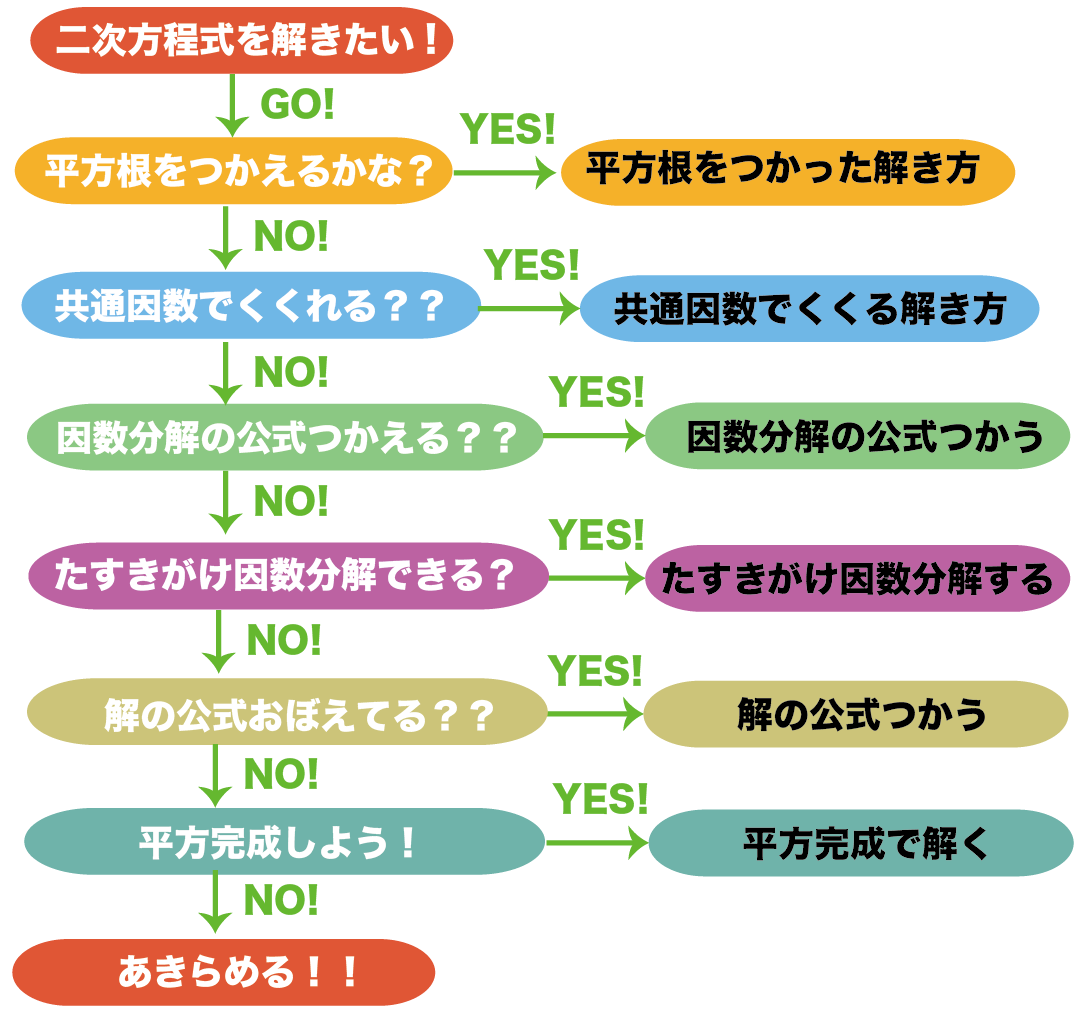



中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく




世界一わかりやすい数学問題集中3 3章 二次方程式




式の展開方法 前2乗全後ろ2乗 X A 2 苦手な数学を簡単に




高校数学 展開のおさらい2 カッコ カッコの公式 例題編 映像授業のtry It トライイット




ルートの外し方 の中に二乗ができたら外すことができる 中学や高校の数学の計算問題



Elu4wv8naj 2gm
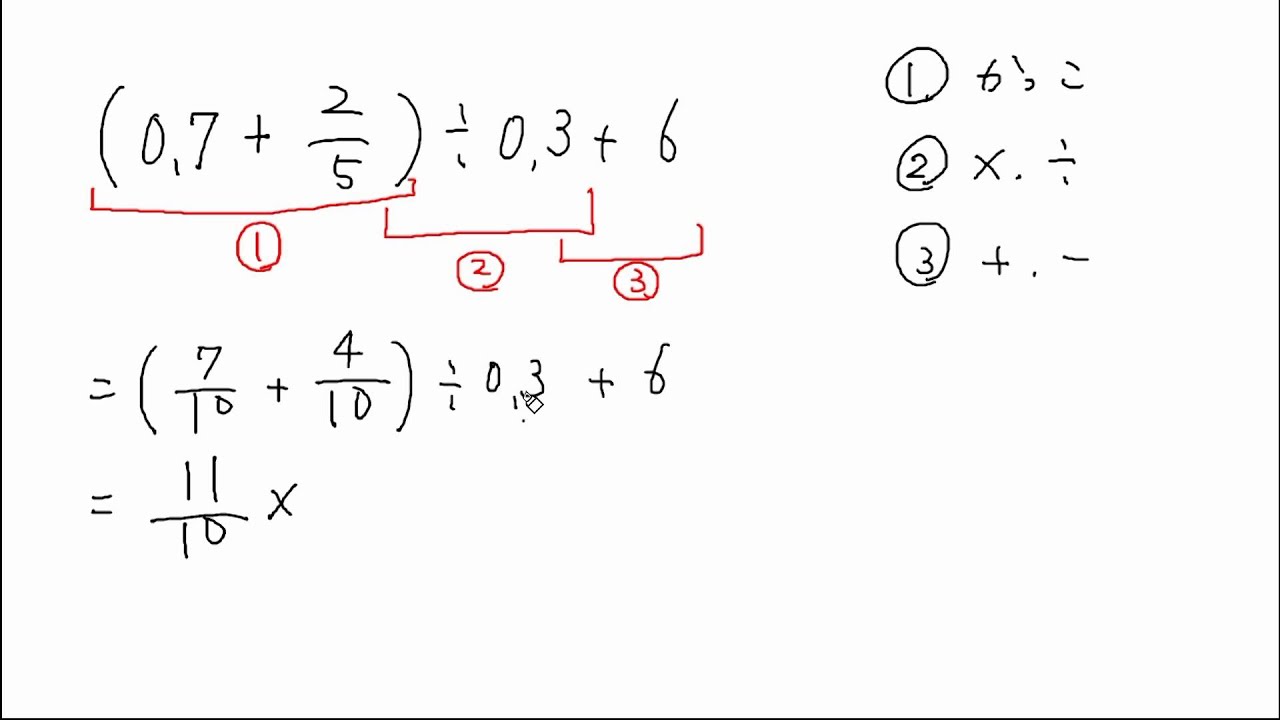



計算まとめ かっこの入った計算 Youtube



かっこの外 二乗 どっちを先に計算するのですか おしえてください Yahoo 知恵袋
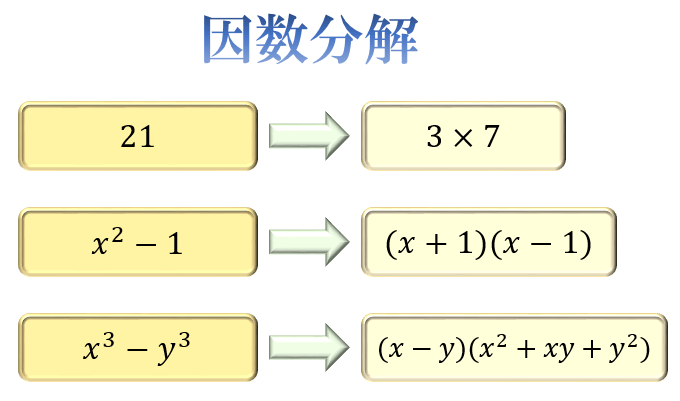



因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ




対称式の変形まとめ 基本公式を覚えてサクサク計算しよう 数スタ



この計算のやり方を教えてください 言葉で書きます かっこマイ Yahoo 知恵袋
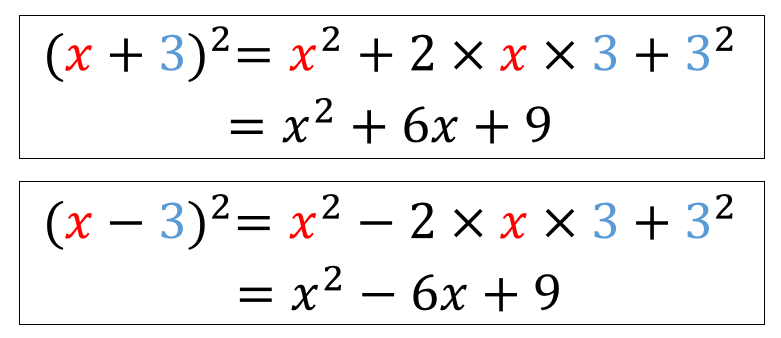



中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ
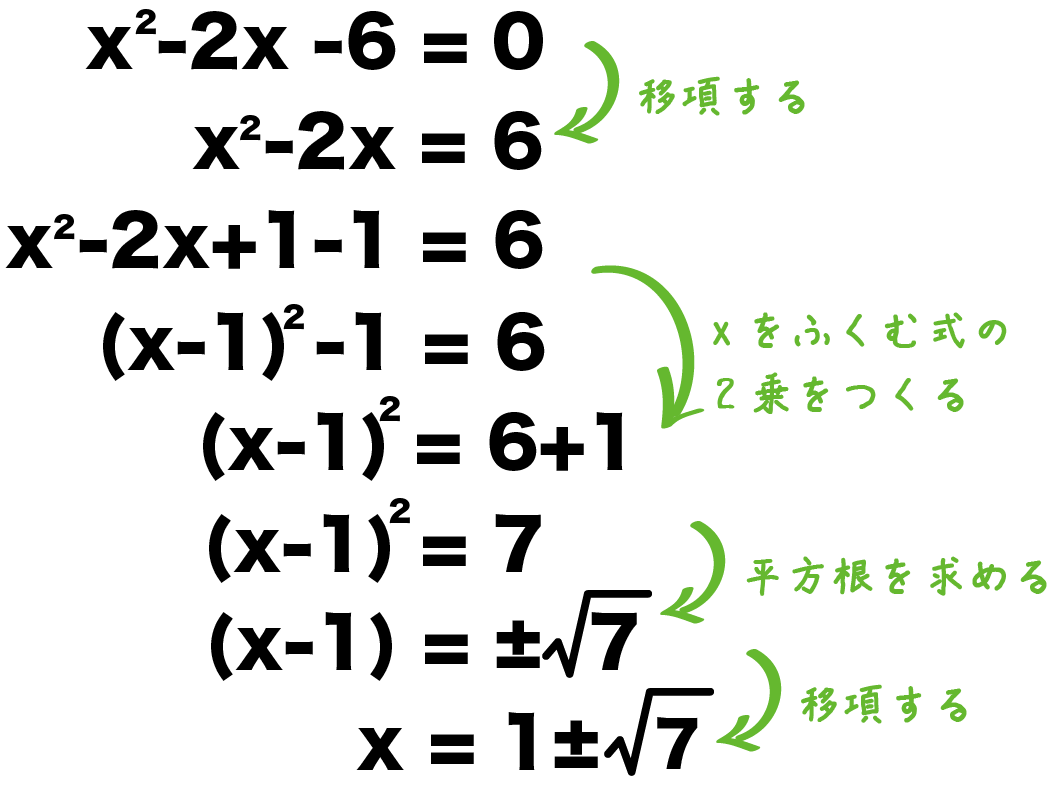



中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく
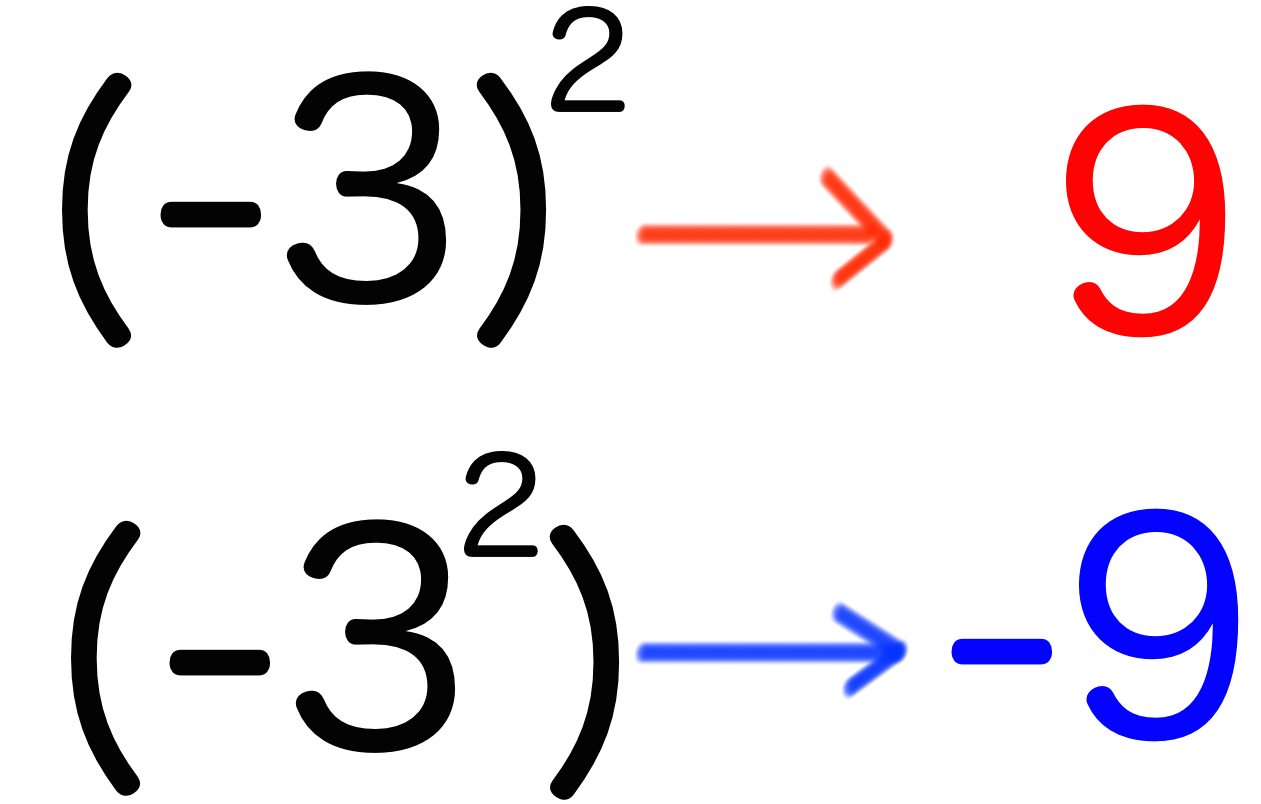



中学数学 指数の計算で注意すべき3つのポイント Qikeru 学びを楽しくわかりやすく




複素数と方程式 の記事一覧 受験辞典




分数の連立方程式 解き方は両辺に数をかけて分母を消すんだ 中学や高校の数学の計算問題
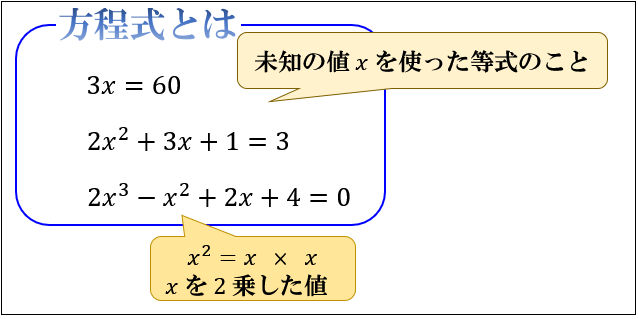



二次方程式の意味と解き方まとめ 解の公式 因数分解 アタリマエ




の中に二乗があるときと の外に二乗がある時の違いを教えてください Clear




二次方程式の意味と解き方まとめ 解の公式 因数分解 アタリマエ




受験あるので早急に知りたいです Clear




二次方程式の解き方 平方根 因数分解 解の公式での答えの求め方 リョースケ大学




数学 A B C 二乗の展開公式は 問題の解き方は徹底解説 数スタ



二次方程式の意味と解き方まとめ 解の公式 因数分解 アタリマエ
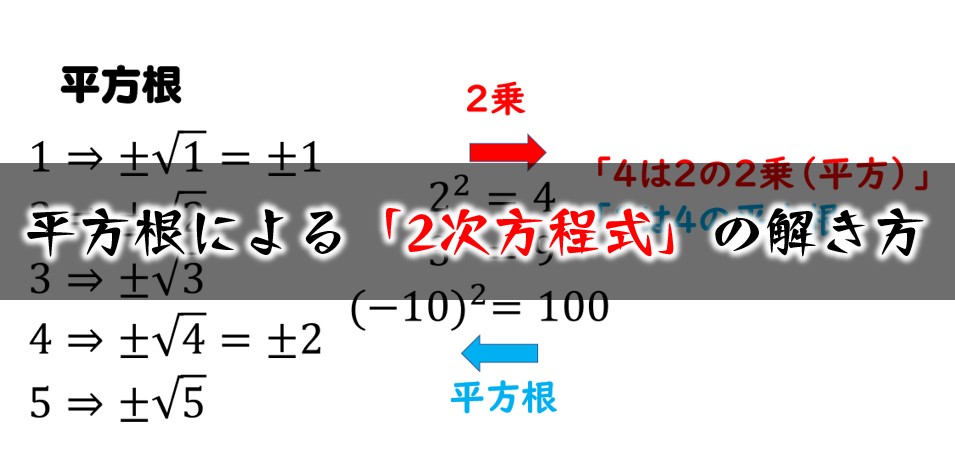



2次方程式の解き方 平方根を利用 数学fun




二次方程式の意味と解き方まとめ 解の公式 因数分解 アタリマエ
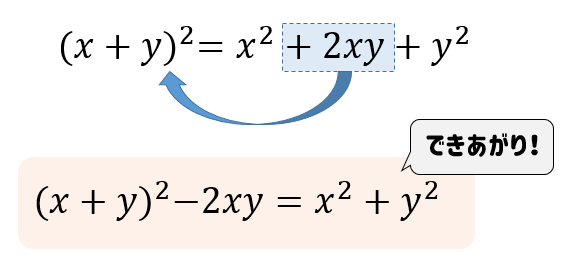



二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ




中学数学 二次方程式




中3数学 問題演習 二次方程式の利用 計算を間違える問題 Youtube




超簡単 二次不等式の解き方が誰でもわかる 必ず解きたい問題付き 高校生向け受験応援メディア 受験のミカタ




平方根についてです Clear



中3数学12 二次方程式2 解き方2平方完成 基本解説プリント 問題 316



展開公式とは 1分でわかる意味 二乗 3乗の公式 覚え方 問題




中学校数学 3年生 数量 2次方程式 Wikibooks



12 X 2カッコ外の2は2乗です 解き方教えて下さい Yahoo 知恵袋




中3数学 カッコ カッコの公式2 X A 2 X A 2 練習編 映像授業のtry It トライイット




この連立方程式の問題なのですがtの二乗になるところがよく分かりません Clear



0 件のコメント:
コメントを投稿